La perspective cavalière
		Utilisation : La perspective cavalière est utilisée en mathématiques pour les dessins géométriques. Elle permet de réaliser des schémas en vue de soutenir un raisonnement. La représentation en perspective cavalière n'est pas conforme à notre vision naturelle des objets. Pourtant celle-ci obéit à des règles de construction précises qu'il convient de respecter dans la réalisation d'un dessin technique. Ainsi, pour dessiner un solide en perspective cavalière il faut distinguer :
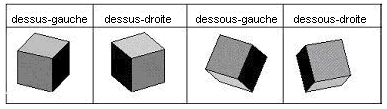
			- Le point de vue : C'est l'endroit où se trouve l'observateur. Pour que l'objet soit représenté avec un certain effet de volume, il faut que l'observateur soit placé un peu à droite ou à gauche sur une droite horizontale (parallèle à la droite d'horizon) et un peu au-dessus ou au-dessous sur une droite verticale (perpendiculaire à la droite d'horizon). Ce qui donne quatre types de points de vue.
			- Les faces frontales : Ce sont les faces situées dans un plan perpendiculaire à notre regard. Ces faces sont dessinées dans leurs formes réelles, à l'échelle. Leurs dimensions (longueur, largeur, hauteur, rayon...) sont conservées. Les angles ont leur mesure réelle.
			- Les faces fuyantes : Ce sont les faces qui forment les côtés. Les segments verticaux sont représentés par des segments verticaux dont les longueurs sont les vraies longueurs. Les mesures des angles ne sont pas conservées (par exemple: des droites perpendiculaires dans la réalité ne le sont plus sur le dessin). Le parallélisme est conservé. Le partage en segments égaux, sur les segments fuyants, est conservé et notamment le milieu. Toutes les droites horizontales de l'objet sont représentées par des droites fuyantes parallèles. Les dimensions sur ces droites fuyantes sont diminuées par le coefficient de fuite. Pour respecter ces règles, on utilise un angle et un coefficient de fuite. Angle de fuite : c'est l'angle que font toutes les droites fuyantes d'une face fuyante, avec l'horizon du dessinateur. Coefficient de fuite : c'est un nombre compris entre 0 et 1 par lequel nous multiplions les dimensions réelles des segments fuyants (sur les droites fuyantes) pour obtenir leurs dimensions sur le dessin.
			Exemple : dessin d'un cube de 36 mm d'arête. L'angle de fuite est 30°. Le coefficient de fuite est 0,5. Point de vue : dessus-droite. Deux faces frontales (devant et derrière), quatre faces fuyantes (dessous, dessus et de chaque côté à droite et à gauche). -Les côtés fuyants sont tous de même longueur (36 x 0,5 = 18 mm) et parallèles. Les deux faces frontales sont en vraie grandeur ainsi que les segments verticaux. Exemple : dessin d'un cube de 36 mm d'arête.
			Bilan sur la perspective cavalière:
			Avantages de la représentation en perspective cavalière : Elle est très simple à réaliser pour les solides usuels délimités par des faces planes. On peut mesurer et calculer simplement des dimensions réelles à partir d'un dessin. Inconvénient de la représentation en perspective cavalière : Elle n'est pas conforme et de ce fait ne conduit pas à des représentations agréables à l'œil, ce qui la disqualifie pour des usages où l'esthétique de la représentation compte. C'est pourquoi une autre perspective est utilisée dans les oeuvres d'arts où l'objectif principale est d'attirer l’œil a travers la beauté de l'ouvrage. Un problème reste toutefois récurrent aux deux formes de perspectives. En effet, la principale difficulté est de représenter les 3 dimensions de la réalité sur un plan a uniquement deux dimensions. C'est pourquoi la découverte d'une perspective qui allie à la fois esthétique et réalisme fut tardive et difficile à adopter pour les contemporains des artistes italiens de la renaissance.
			<< | < | > | >>