![]() Les illusions
dues à des effets d’angles sont très nombreuses et
elles sont sans doute parmi les plus spectaculaires. On s’est appuyé
sur deux principes pour les expliquer. D’une part, l’on a tendance
à surestimer les angles aigus et à sous-estimer les angles
obtus. On a qualifié ceci de principe d’orthogonalité,
étant donné qu’il s’agit dans chaque cas d’une
tendance à ramener l’angle vers un angle droit. Ce principe
permet d’expliquer aisément les illusions de Zöllner
et de Hering, mais il peut aussi s’appliquer à l’illusion
de Poggendorff et à celle de Müller-Lyer. Le second principe
concerne la tendance que l’on a à surestimer les côtés
d’un angle obtus et à sous-estimer ceux d’un angle aigu.
Les illusions
dues à des effets d’angles sont très nombreuses et
elles sont sans doute parmi les plus spectaculaires. On s’est appuyé
sur deux principes pour les expliquer. D’une part, l’on a tendance
à surestimer les angles aigus et à sous-estimer les angles
obtus. On a qualifié ceci de principe d’orthogonalité,
étant donné qu’il s’agit dans chaque cas d’une
tendance à ramener l’angle vers un angle droit. Ce principe
permet d’expliquer aisément les illusions de Zöllner
et de Hering, mais il peut aussi s’appliquer à l’illusion
de Poggendorff et à celle de Müller-Lyer. Le second principe
concerne la tendance que l’on a à surestimer les côtés
d’un angle obtus et à sous-estimer ceux d’un angle aigu.

Illusion de Zöllner
Les lignes obliques ne semblent pas parallèles, alors qu’elles
le sont. Elles nous paraissent déformées à cause
des petites lignes qui forment le graphisme secondaire.
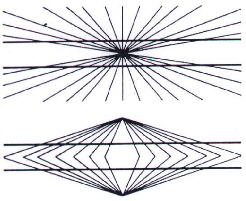
Les lignes horizontales semblent incurvées, alors qu’elles sont physiquement droites et parallèles.

Le segment oblique inférieur ne paraît pas dans l’axe du segment oblique supérieur, alors que physiquement ils sont dans le même axe.