|
|
|
 La
raison pour laquelle les personnes sont surprises devant ces figures est
dû à un a priori. Souvent elles pas réalisent même
qu'elles ont fait cette supposition. La supposition est que nous comparons
deux triangles, et qu'elles chacune ont la même aire. Certainement
une inspection rapide - aidée par la grille – nous affirme que
les 'triangles’ sont de 13 carreaux de base sur 5 de haut, et qu’ils
se ressemblent. La
raison pour laquelle les personnes sont surprises devant ces figures est
dû à un a priori. Souvent elles pas réalisent même
qu'elles ont fait cette supposition. La supposition est que nous comparons
deux triangles, et qu'elles chacune ont la même aire. Certainement
une inspection rapide - aidée par la grille – nous affirme que
les 'triangles’ sont de 13 carreaux de base sur 5 de haut, et qu’ils
se ressemblent.
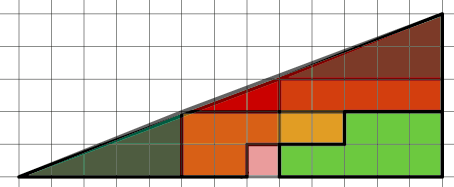
 En fait le triangle
supérieur n'est pas un triangle du tout : c’est un tétraèdre.
Si vous regardez attentivement la ligne de l’hypoténuse (la
diagonale), vous verrez qu'il n'est pas tout à fait droit, il est
légèrement concave. Pourquoi ? Tout simplement car le triangle
vert-foncé a une base de 5 carreaux et une hauteur de 2. Le triangle
rouge, possède lui une hauteur de 3 carreaux, et devrait avoir une
base de 7.5 pour que l’hypoténuse ait le même angle avec
l'horizontal. En fait le triangle
supérieur n'est pas un triangle du tout : c’est un tétraèdre.
Si vous regardez attentivement la ligne de l’hypoténuse (la
diagonale), vous verrez qu'il n'est pas tout à fait droit, il est
légèrement concave. Pourquoi ? Tout simplement car le triangle
vert-foncé a une base de 5 carreaux et une hauteur de 2. Le triangle
rouge, possède lui une hauteur de 3 carreaux, et devrait avoir une
base de 7.5 pour que l’hypoténuse ait le même angle avec
l'horizontal.  En
fait le triangle rouge a une base de 8 carreaux, et l'angle de l’hypoténuse
est légèrement plus peu profond qui celui du triangle vert-foncé.
Voilà pourquoi l’hypoténuse n’est pas une ligne
droite, quand vous regardez soigneusement. En
fait le triangle rouge a une base de 8 carreaux, et l'angle de l’hypoténuse
est légèrement plus peu profond qui celui du triangle vert-foncé.
Voilà pourquoi l’hypoténuse n’est pas une ligne
droite, quand vous regardez soigneusement.
 Le 'triangle
'inférieur n'est pas une triangle non plus, c'est également
un tétraèdre, mais maintenant l’hypoténuse est
légèrement convexe, puisque la position des triangles rouge
et vert est maintenant renversée. Le 'triangle
'inférieur n'est pas une triangle non plus, c'est également
un tétraèdre, mais maintenant l’hypoténuse est
légèrement convexe, puisque la position des triangles rouge
et vert est maintenant renversée.
 Voici une image
des deux triangles superposés, qui montre la différence des
deux l’hypoténuse : Voici une image
des deux triangles superposés, qui montre la différence des
deux l’hypoténuse : |
|
|
|